“Deviazione standard” è una di quelle espressioni statistiche spesso usate senza capirne veramente il significato. Se vi fosse capitato, oggi potete smettere di vivere di menzogna 😉 .
Nell’articolo di oggi, imparerete come questa misura statistica sottovalutata possa aiutare a capire meglio i dati su cui si sta lavorando.
Cosa è la deviazione standard
Immaginate di supervisionare due responsabili di reparto che vendono ricotta. Dal momento che non volete sprecare nessuna confezione di ricotta, è importante che questi due responsabili abbiano un inventario aggiornato costantemente. Nel tentativo di misurare quanto bene gestiscano gli ordini, decidete di analizzare gli scatoloni di ricotta che ciascun responsabile ha ordinato nelle ultime sei settimane. Prendendo la media delle ultime 6 settimane, è possibile vedere che ogni responsabile ordina una media di circa 42 scatoloni di ricotta a settimana. Ad un’analisi superficiale, le medie fanno sembrare che la loro gestione sia simile.
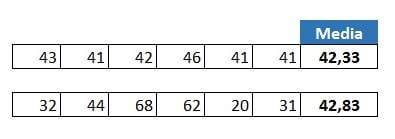
Ma se guardate più da vicino, vedrete che uno dei responsabili ha ordini settimanali di 32, 44, 68, 62, 20 e 31 scatoloni. Per questo gestore, la media può essere matematicamente corretta, ma nasconde la volatilità dei suoi ordini settimanali. In altre parole, a volte la media di un insieme di dati non rappresenta correttamente i dati. È qui che entra in gioco la deviazione standard.
La deviazione standard dà un’idea di come siano distribuiti i dati nel campione rispetto alla media. Detto in un altro modo – consente di sapere se la media è affidabile per dare una rappresentazione significativa dei dati.
Nel nostro esempio, usiamo la funzione DEV.ST.C in Excel in modo da affiancare la Deviazione standard alla nostra Media.
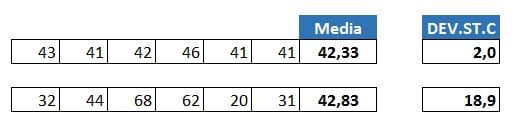
Nel caso del primo responsabile, la deviazione standard è 2. Questo ci dice che ogni dato del campione si trova a una distanza media di 2 punti dalla media. È una cosa buona? Beh, pensate in questo modo – una deviazione standard di 0 starebbe a significare che ogni dato è esattamente uguale alla media del campione (42,33 in questo caso). Una deviazione standard di 2 non è così lontana da 0, indicando che la maggioranza dei dati è posizionata molto vicino alla media. Quanto più la deviazione standard è vicina a 0, quanto più affidabile è la media. Quindi una deviazione standard vicina a 0 ci dice che c’è poca volatilità nel campione. Con una deviazione standard di 2, gli ordini settimanali del primo gestore sono notevolmente coerenti.
Nel caso del secondo gestore, la deviazione standard è 18,9. La distanza media di ogni dato è distante dalla media di 18,9 punti. Questa è una differenza enorme! Significa che per questo campione di dati la media di 42,83 scatoloni a settimana non è affidabile. Essa indica inoltre che gli ordini settimanali di questo gestore sono estremamente volatili. Naturalmente, con una rilevazione di sole 6 settimane, sarebbe possibile confermare tale volatilità anche con la semplice osservazione.
Questa, in poche parole, è la Deviazione standard. Anche se non riscuote lo stesso successo di altre misure statistiche (media, mediana, moda, ecc), la deviazione standard è in realtà fondamentale per molti calcoli statistici. Capire come funziona la deviazione standard vi potrebbe spianare la strada nel realizzare cose come: determinare la volatilità di un titolo, normalizzare il confronto tra gruppi di dati, identificare i valori anomali e molto altro.
Come è calcolata la deviazione standard
Ok, sappiamo cosa mostra la deviazione standard. Ora diamo un’occhiata a come in realtà è calcolata.
Inizieremo con questa serie di numeri (in nero). Come potete vedere, ho già usato la funzione DEV.ST.C per calcolare la deviazione standard di 21,6 (in rosso).

Ecco i passaggi che Excel ha effettuato per calcolare 21.6 come la deviazione standard.
In primo luogo, Excel calcola la media per il campione. In questo caso, la media è 40. quindi calcola la differenza tra ciascun dato e 40. Per esempio, la differenza tra 50 e 40 è +10 punti. La differenza tra 10 e 40 è -30.
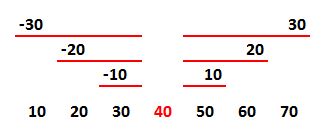
La cosa che Excel fa poi è elevare al quadrato tutte queste differenze in modo che tutte siano un numero positivo (+10 diventa 100; -30 diventa 900).

Excel somma poi tutte le differenze quadratiche per ottenere la differenza quadratica totale:
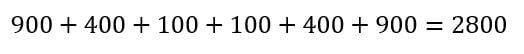
Poi, Excel utilizza la differenza quadratica totale per calcolare la varianza campionaria. Questo viene fatto dividendo il totale delle differenze quadratiche per il conteggio dei dati nel campione meno 1. In questo esempio il numero di dati è 7, quindi il totale delle differenza quadratiche va diviso per 7-1:
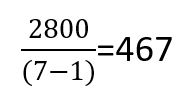
Infine Excel calcola la radice quadrata della varianza campionaria, per ottenere la nostra deviazione standard:
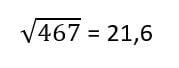
Deviazione standard della popolazione e deviazione standard del campione
In statistica, spesso si sentono termini come popolazione e campione. Questi termini si riferiscono alla completezza dei dati in vostro possesso. Le differenze tra i due a volte non sono chiare.
Se state usando un set di dati completo, state utilizzando una popolazione. Un esempio di una popolazione potrebbero essere i dati per tutti i responsabili di vendita che esistono nella vostra azienda; una popolazione totale.
Se state utilizzando un set parziale di dati o un sottoinsieme di dati, avete a che fare con quello che viene chiamato un campione. Un esempio potrebbe essere se state analizzando i dati di vendita per un solo trimestre di un anno. Un trimestre è solo un sottoinsieme dei dati di un intero anno, quindi in questo caso, state lavorando con un campione.
Il motivo per cui questa distinzione è importante è perché il calcolo per la deviazione standard cambia leggermente a seconda della natura dei dati che state trattando. In particolare, il modo di calcolare la varianza campionaria. Abbiamo detto che Excel divide le differenze quadratiche totali per il conteggio dei dati del campione meno 1. Bene, questo vale solo se i dati sono un campione (un sottoinsieme di un set di dati più grande). Se i dati sono tutta la popolazione, non è necessario sottrarre 1. Questo porterebbe ad avere una deviazione standard diversa.

Allora, perché questa differenza di calcolo? Beh, la differenza non è un capriccio di Excel. Si tratta di un concetto statistico chiamato “Correzione di Bessel”. La “Correzione di Bessel” afferma che quando si utilizza un campione di un set di dati, invece di una intera popolazione, è necessario sottrarre 1 dal conteggio dei dati utilizzati (ciò viene scritto in gergo statistico come n-1). Il ragionamento che sta dietro alla necessità di questa correzione è un po’ difficile per noi che non siamo dei matematici, pertanto non cercherò di spiegarlo.
Le funzioni che calcolano la deviazione standard in Excel
Excel ha la capacità di gestire i calcoli della deviazione standard sia per l’intera popolazione che per un campione di essa. Basta fare clic in una cella e iniziare a digitare =DEV.ST. Vedrete un menu a discesa con alcune funzioni di deviazione standard.
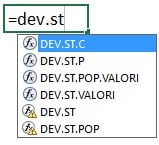
Ecco un breve riassunto di ciò che ogni funzione fa.
- DEV.ST.C – Calcola la deviazione standard di un campione utilizzando la Correzione di Bessel (n-1). Questa funzione sostituisce tecnicamente la funzione DEV.ST
- DEV.ST.P – Calcola la deviazione standard per una popolazione. Questa funzione sostituisce tecnicamente la funzione DEV.ST.POP
- DEV.ST.POP.VALORI – Calcola la deviazione standard per una popolazione. Permette l’utilizzo di valori di testo e valori logici VERO/FALSO
- DEV.ST.VALORI – Calcola la deviazione standard di un campione utilizzando la Correzione di Bessel (n-1). Permette l’utilizzo di valori di testo e valori logici VERO/FALSO
- DEV.ST – Calcola la deviazione standard di un campione utilizzando la Correzione di Bessel (n-1). È stata mantenuta per ragioni di compatibilità, pur essendo stata sostituita dalla più recente funzione DEV.ST.C
- DEV.ST.POP – Calcola la deviazione standard per una popolazione. È stata mantenuta per ragioni di compatibilità, pur essendo stata sostituita dalla più recente funzione DEV.ST.P
Non riesco ad immaginare uno scenario in cui utilizzare le funzioni DEV.ST.POP.VALORI e DEV.ST.VALORI. Penso che possiate ignorarle tranquillamente.
Per quanto posso dire, non vi è alcuna differenza tra il DEV.ST.C e DEV.ST. Microsoft suggerisce di spostarci verso la più recente funzione DEV.ST.C, ma tecnicamente è possibile utilizzare queste due funzioni in modo intercambiabile.
Allo stesso modo, non vedo alcuna differenza visibile tra DEV.ST.P e DEV.ST.POP. Anche se DEV.ST.P è la funzione più recente, è possibile utilizzare queste due funzioni in modo intercambiabile.


